二次函數頂點坐標(配方法二次函數頂點坐標)

在中考數學眾多試題當中，函數與幾何有關的試題是我們必須要重點關注的對象，它不僅能很好考查考生基礎知識和方法技巧的掌握程度，更能考查考生分析問題和解決問題的能力，屬于綜合應用題。

函數與幾何有關的試題作為中考數學的必考重難點，在中考里占據著重要的位置，毫不夸張的說全國各地中考壓軸題都屬于此類題型。在解函數與幾何有關試題的時候，大家一定要明白一點，此類綜合問題不像求解單純幾何問題或單純函數問題那么簡單，需綜合考慮函數知識與幾何知識之間的內在聯系。

如在一些問題里需考慮幾何元素之間的函數關系問題，解這類問題應根據幾何圖形的性質，建立函數與自變量表示的幾何元素之間的等量關系等。或者是先根據函數解析式求出有關點的坐標(如圖像與坐標軸交點，兩圖像交點等)，其次依據點的坐標求出有關線段的長度，最后利用有關定理、性質、公式即可使問題獲解。

在中考數學里，函數與幾何有關的綜合問題一直是讓考生非常頭疼的試題，它既是重難點問題，又是考查學生分析問題和解決問題的能力問題。要想成功解決此類問題，考生除了加強訓練，還要培養良好的解題習慣，注重思維方法的訓練，理解數形結合思想方法等，定能順利解決問題。

同時，函數與幾何有關的綜合問題蘊含著豐富的數學思想方法，如數形結合思想。數形結合是在研究問題時把數和形結合起來考慮，或者把問題的數量關系轉化為圖形的性質，或者把圖形的性質轉化為數量關系，從而使復雜的問題簡單化，抽象的問題具體化。通過直角坐標系這個工具，有機地進行數形轉換，如在解函數與幾何的綜合題，先求出點的坐標，進而求出函數解析式是解題的基礎，同時充分發揮形的因素，實現數形互動，通過坐標把證明與計算相結合是解題的關鍵。

函數與幾何有關的綜合問題分析，典型例題1：

己知：二次函數y=ax2+bx+6（a≠0）與x軸交于A、B兩點（點A在點B的左側），點A、點B的橫坐標是一元二次方程x2﹣4x﹣12=0的兩個根．

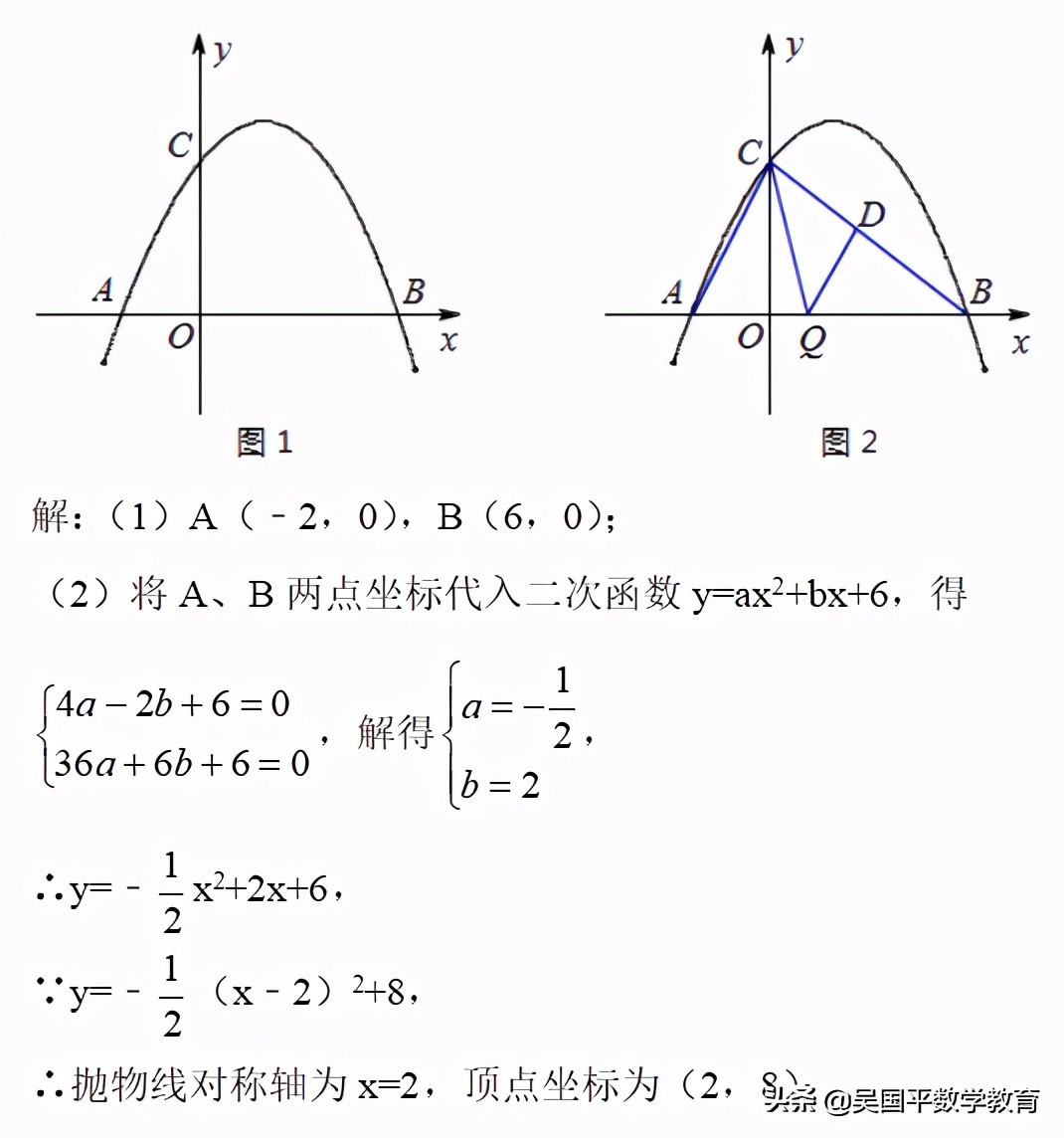
（1）請直接寫出點A、點B的坐標．

（2）請求出該二次函數表達式及對稱軸和頂點坐標．

（3）如圖1，在二次函數對稱軸上是否存在點P，使△APC的周長最小，若存在，請求出點P的坐標；若不存在，請說明理由．

（4）如圖2，連接AC、BC，點Q是線段0B上一個動點（點Q不與點0、B重合）．過點Q作QD∥AC交BC于點D，設Q點坐標（m，0），當△CDQ面積S最大時，求m的值．

考點分析：

二次函數綜合題；綜合題。

題干分析：

（1）解一元二次方程x2﹣4x﹣12=0可求A、B兩點坐標；

（2）將A、B兩點坐標代入二次函數y=ax2+bx+6，可求二次函數解析式，配方為頂點式，可求對稱軸及頂點坐標；

（3）作點C關于拋物線對稱軸的對稱點C′，連接AC′，交拋物線對稱軸于P點，連接CP，P點即為所求；

（4） 由DQ∥AC得△BDQ∽△BCA，利用相似比表示△BDQ的面積，利用三角形面積公式表示△ACQ的面積，根據S△CDQ=S△ABC﹣S△BDQ﹣S△ACQ，運用二次函數的性質求面積最大時，m的值．

解題反思：

本題考查了二次函數的綜合運用．關鍵是根據已知條件求拋物線解析式，根據拋物線的對稱性，相似三角形的知識解題。

在解決此類問題的時候，我們可以利用函數圖像，結合幾何圖形的性質，通過坐標這個特殊量把“形”和“數”進行完美結合，體現了數形結合的思想方法。在解決問題的過程中，大家觀察圖形主要是觀察圖形的形狀、大小、位置關系等，尋找圖形中蘊含的數量關系，從而求得坐標，運用推理或計算得出結論，借助圖形的幾何直觀來闡明函數變量之間的某種關系能使問題簡單。

同時函數與幾何有關的綜合問題會把函數、方程、不等式等知識聯系起來，求解的關鍵是要深挖圖形的幾何意義，以形為手段，數為目的，依靠形的直觀具體，借助坐標來表明數式之間的關系。

函數與幾何有關的綜合問題分析，典型例題2：

如圖，已知拋物線經過定點A（1，0），它的頂點P是y軸正半軸上的一個動點，P點關于x軸的對稱點為P′，過P′作x軸的平行線交拋物線于B．D兩點（B點在y軸右側），直線BA交y軸于C點．按從特殊到一般的規律探究線段CA與CB的比值：

（1）當P點坐標為（0，1）時，寫出拋物線的解析式并求線段CA與CB的比值；

（2）若P點坐標為（0，m）時（m為任意正實數），線段CA與CB的比值是否與（1）所求的比值相同？請說明理由．

考點分析：

二次函數綜合題．

題干分析：

（1）根據拋物線經過A（1，0），設拋物線的解析式為y=ax2+1，首先得出二次函數解析式，進而得出P&39;點的坐標，從而得出B點坐標，再利用△CP′B∽△COA，得出線段CA與CB的比值；

（2）根據設拋物線的解析式為y=ax2+m（a≠0），得出y=﹣mx2+m，首先表示出B點的坐標，進而利用△CP′B∽△COA，得出線段CA與CB的比值．

解題反思：

此題主要考查了二次函數的綜合應用以及相似三角形的性質，得出根據P′B=√2，再利用△CP′B∽△COA，得出是解決問題的關鍵．

數與形是數學學習中兩個最基本的兩個量，它們之間可以相互轉化，將問題化難為易，化抽象為具體。函數與幾何有關的綜合題恰好體現了數形結合之間的關系，解題關鍵就是準確深刻理解函數與幾何圖形結合，即點的坐標，由坐標體現為長度、角度，或是由長度轉化為坐標，也即說數形結合轉換離不開坐標。

在函數關系式下求解析式問題，或是在幾何圖形下求幾何問題，這類型問題的解決方法是圖形坐標化，通過坐標這個切入點，架起數到形的橋梁，由數量關系來研究幾何圖形的性質，解決幾何問題是以函數為背景探求幾何性質，利用函數的性質，解決幾個主要點的坐標問題，使幾何知識和函數知識有機而自然地結合起來。

善于利用平面直角坐標系，就可以實現從數到形，也可從形到數，即觀察圖形的形狀，分析數與式的結構，適時通過坐標將它們相互轉換，化抽象為直觀并提示隱含的數量關系，大大減輕了數形轉換的難度。

函數與幾何有關的壓軸題，一直是近年來中考數學命題的熱點 這類試題知識點眾多，解法靈活，形式多樣，綜合性強，難度大，要求大家具有很強的分析推理能力。

縱觀近幾年各地中考試卷中的函數與幾何壓軸題，從知識結構來看可分為兩大類型，即幾何含函數型和函數含幾何型，這類題目是以幾何圖形為載體，求幾何圖形中某些幾何量之間的函數關系式．其解題方法是利用幾何圖形的有關性質，列出幾何元素之間的等量關系，并將這種關系轉化成函數關系，最后利用函數的性質解答問題。